Decibel bemutató: dB és dBm vs Gain és Milliwat

A decibel (dB) fogalma érthetően nehéz és zavaró valaki számára, akit csak bevezettek vele. A dB, dBm, dBW, watt, milliwatt, feszültség, millivolt stb. Keveréséhez szükséges erősítésre, teljesítményre és feszültségre (és áramra, de nem olyan gyakran) vonatkozó előírások egyesítésekor gyakran szükség van a lineáris értékek és a decibel értékek közötti oda-vissza konvertálásra. Ez a rövid bemutató segít tisztázni a különbséget a decibellekkel végzett munka és a lineáris értékekkel való munka között.

A logaritmusokat (naplókat) először a 1600 korai szakaszában a skót matematikus, John Napier fejlesztette ki, mint olyan eszközt, amely egyszerűsíti a szorzási és osztási műveleteket oly módon, hogy gyorsabb és kevésbé hibára hajlamos összeadási és kivonási műveletekké konvertálják őket. Ez azért lehetséges, mert a két alapszámon kifejezett számok szorzata az exponensekkel egyszerűen az exponensek összeadásával érhető el. Ugyanazon számok felosztása az exponensek kivonásával történik. Ez az exponensek egyik törvénye, és így néz ki:

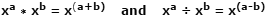
Például a tényleges számok felhasználásával, ahol x = 10, a = 4, b = 1:

Az exponensek törvénye az alapszámokra vonatkozik, nem csak az 10-re. Szerelem:

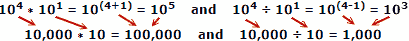
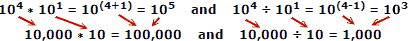
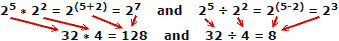
Az emberek általában kevesebb hibát követnek el számok összeadásakor és kivonásakor, tehát a logaritmus előnye nyilvánvaló. Ne feledje, hogy a logaritmusokat még azelőtt dolgozták ki, hogy automatikus mechanikus vagy elektronikus számítógépek rendelkezésre álltak. A csúszó szabály kihasználja a logaritmus tulajdonságait a számításhoz, de ez külön külön téma.

Ezek egyszerű példák, de minden bázison vagy exponensen érvényesek. Számológép hiányában ahhoz, hogy az általános alkalmazásban hasznos legyen, szüksége van egy számtáblára és azokkal egyenértékű logaritmusokra. A korai naplózótáblák kitöltött kötetek, a számok közötti távolságtól függően (1.000, 1.001, 1.002, 1.003, vs. 1.0, 1.1, 1.2, 1.3 stb.). A jó hír a logaritmustáblák készítői számára, hogy csak egyetlen számú „évtizedre” van szükség (pl. 1 – 10), mivel minden előző vagy azt követő évtized az 10 teljesítményének egyszerű szorzata.

Megjegyzés: Az 10 alapot használom ebben a beszélgetésben, mivel ez a közös számrendszerünk alapja - ebből következően a „közös logaritmus” kifejezés az alap 10 naplókra. Lehet, hogy hallottál a természetes logaritmusokról, amelyek az e alapját használják, de az e-t nem gyakran használják a skaláris elektromos teljesítmény, feszültség és árammennyiségek kiszámításakor (bár ezt használják fázisszögek beszámításánál, azaz az Euler-féle identitásnál). A természetes logaritmusokat ln (x) -ként írják, az 'e' alindex nélkül, míg az alap 10 logaritmusokat egyszerűen log (x) -ként írják, az 10 alszám nélkül; azaz nem loge (x) vagy log10 (x).

Alaponként = 10 naplózási táblázat:

Félig logaritmikus 5 ciklusmérnöki grafikus papír - RF CafeA kivétel és különleges eset a logx (0) = nincs meghatározva. Ez azért van, mert nincs olyan hatalom, amelyhez bármilyen számot fel lehet emelni, és 0-t (nullát) szerezhet. Aszimptotikusan megközelítheti a nullát, de nullához nem juthat el. Soha nem jelenik meg a nulla szám a napló skálán; általában az 10 valamilyen teljesítményétől a tíz másik teljesítményig terjednek. A naplógrafikon papír példája látható a jobb oldalon. 5 „ciklusok” vagy „évtizedek” tartományban van. Vegye figyelembe, hogy az y tengelyen nulla nincs.

A szám alap-10 (általános) logaritmusa tehát az az exponens, amelyre az 10-t fel kell emelni annak érdekében, hogy megkapja ezt a számot. Más szavakkal, mivel az 10 teljesítménnyel megemelt 2 értéke megegyezik az 100 értékkel (102 = 100), az 10 alap-100 naplója 2 (log10 100 = 2).

Ez a logaritmus alaptétele:


Végezzük el ugyanazokat a szorzatokat és osztásokat, mint amelyeket az oldal tetején hajtunk végre a tényleges logaritmus segítségével:



Nagyszerű, de végül a kívánt szám logaritmusa van. Kérdés: Egy egyszerű példa kivételével hogyan kapja meg a szükséges választ? Válasz: Keresse meg az eredmény antilogaritmusát (antilog). Ebben az esetben:

Egy keményebb és valószínűbb példa olyan számokkal, amelyek nem az 10 egész számjai, az alábbiak szerint nézhet ki:




 HP-35 számológép (wikipedia) - RF CafeAmivel az 'x' logaritmusa megegyezik az 1.8444 értékkel, az antilog egyenlő 'x' -vel, amely 69.9



A számológéppel kerestem a számok naplóit és antilogjait, de az 1972 előtt, amikor a Hewlett Packard (HP) bemutatta a HP-35 tudományos számológépet, az átlagos személynek nincs hozzáférése a vállalati vagy egyetemi nagyszámítógépes számítógéphez a napló használatához. táblázat az ilyen számítások elvégzéséhez.

Felteheti a kérdést, hogy ki zavarja ma a logaritmus használatát? Sok ember, köztük én is, elég gyakran olyan lépcsőzetes rendszerparaméterek kiszámításakor, mint a zajszint (NF) és az elfogási pontok (IP). A nyereség dB és teljesítmény dBm értékek egyszerű összeadása és kivonása nem működik az NF és az IP esetén. A szabályozó képletek a lineáris nyereség és teljesítmény értékek szorzását és osztását használják, amelyhez először a dB és / vagy dBm lineáris számokra (erősítési arány és mW) konvertálására van szükség antilogok segítségével, a kaszkád számítások elvégzésére, majd az eredmény konvertálására dB és / vagy dBm naplók használatával.

Nem minden rendszer-kaszkád művelet igényli oda-vissza konvertálást. Például, ha csak a teljes rendszererõsítésre és / vagy a kimeneti teljesítményszintre van szükség, akkor a számításokat elvégezhetjük akár lineáris egységekkel (mW és szorzók), akár logaritmikus egységekkel (dBm és dB).

A 'dB' és 'dBm' meghatározása

Az elektrotechnikában a decibelt (dB) úgy kell meghatározni, hogy az 10 az alap-10 logaritmus szorzata és a két teljesítményszint közötti arány; Pl. Pout / Pin (más szóval nyereség). Szerelem:

Az 1-nél nagyobb összes nyereséget ezért pozitív decibellel (> 0), az 1-nél kisebb nyereséget pedig negatív decibellel (<0) fejezzük ki. Ne feledje, hogy a legtöbbünk által tapasztalt esetekben a P1 / P2 lineáris arányának pozitív számnak kell lennie (> 0), mivel a 0 logaritmusa nincs meghatározva, és a negatív számok logaritmusa összetett (tartalmaznak valós és képzeletbeli részt is) ). A dB értéke azonban elméletileg bármilyen értéket felvehet −∞ és + ∞ között, beleértve a 0 értéket is, ami 1 [10 * log (1) = 0 dB] erősítést jelent.

'dBm' egy decibel alapú teljesítményegység, amelyre az 1 mW vonatkozik. Mivel az 0 dB nyereség megegyezik az 1 nyereséggel, az 1 mW teljesítmény 0 dB nagyobb, mint 1 mW vagy 0 dBm. Hasonlóképpen, a dBW teljesítmény egység decibelek az 1 W teljesítményhez viszonyítva.


Ennek megfelelően az 0-nál nagyobb dBm-értékek nagyobb, mint 1 mW, és az 0-nél kisebb dBm-értékek kisebbek, mint 1 mW (lásd az 1. Ábrát). Például a + 3.01 dBm 3.01 dB nagyobb, mint 1 mW; Vagyis, vagy 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). −3.01 dBm 3.01 dB kisebb, mint 1 mW; Vagyis, vagy 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

Az alábbi táblázat néhány numerikus példát mutat, így láthatja az mW és a dBm közötti összefüggést. Ugyanaz az értékkészlet, amelyet logaritmikus skálán ábrázoltak, egyenes lesz. A logaritmikus kapcsolat miatt a gráf a kisebb értékeket a bal oldali függőleges tengelyhez köti. Az 0 – 1 mW régiók nagyított változata be van építve az egyértelműség érdekében.

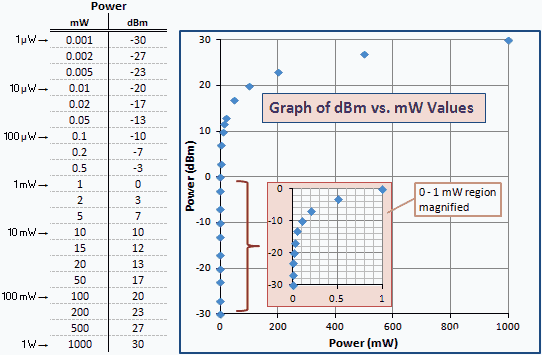
1 ábra - A teljesítmény grafikonja mértékegység dBm-ben mw-ban kifejezve

Az 2 ábra a dB és a lineáris erősítési arányok táblázata és grafikonja, hasonló a dBm és mW értékhez az 1 ábrán. Vegye figyelembe, hogy a számok és a görbék pontosan megegyeznek; csak a tengelycímkék változnak. Ennek oka az, hogy a dBm a teljesítmény egység dB-ben kifejezve az 1 mW (0 dBm) viszonylatában.

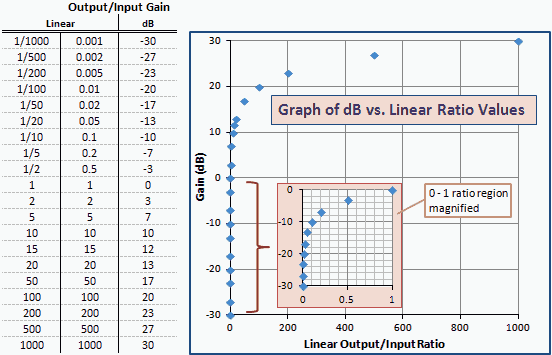
2 ábra - A nyereség grafikonja dBm mértékegységben és a lineáris aránnyal szemben

Alapvetően a nyereség szorzó (vagy osztási) tényező. Például egy erősítőnek lehet olyan erősítése, amely növeli a jelet 4 tényezővel (azaz 4x) a bemenetről a kimenetre (lásd az 3 ábrát). Ha 1 mW (0 dBm) jelet vezet az erősítőbe, akkor 1 mW * 4 = 4 mW jön ki. A decibelek szempontjából az 4 tényező egyenlő 10 * log (4) = 6.02 dB-vel, tehát 0 dBm plusz 6.02 dB-vel a nyereséghozamhoz + 6.02 dBm a kimeneten.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

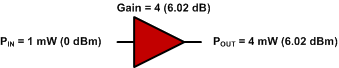
3 ábra - Egyerősítő erősítés.

Kombinált nyereség (lineáris és dB) pozitív értékkel

Ha az 4 erősítéssel rendelkező erősítő egy sorban van egy második erősítővel, amelynek 6 erősítése van, akkor a teljes erősítés 4 * 6 = 24. A decibelben kifejezett 6 tényező egyenértékű 10 * log (6) = 7.78 dB-vel, és az 24 tényező egyenértékű 10 * log (24) = 13.8 dB-vel.

Csakúgy, mint 4 x 6 = 24 (lineáris erősítés), 6.02 dB + 7.78 dB = 13.8 dB (decibel erősítés).

Ha 1 mW jelet (0 dBm) adagolunk az erősítőbe, akkor az 4 mW jön ki az első erősítőből, az 24 mW pedig a második erősítőből. Lásd az 4 ábrát.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

4 ábra - Kaszkádos kettős erősítő nyereség.

Gain és veszteség kombinálása (lineáris és dB)
Ez a következő példa megmutatja, mi történik, ha <1 (veszteség) erősítéssel találkozunk, ahol egy 1/6 erősítésű csillapítót helyezünk az első erősítő után, ahelyett, hogy lenne egy második erősítője. Lásd az 5. ábrát.
4 * 1 / 6 = 2 / 3 (lineáris erősítés). Hasonlóan 6.02 dB - 7.78 dB = −1.76 dB (decibel erősítés).
Az előző példához hasonlóan, ha egy 1 mW jelet (0 dBm) táplálunk az erősítőbe 4 erősítéssel, akkor az 4 mW jön ki. Ez az 4 mW ezután megy a csillapítóba 1 / 6 lineáris nyereséggel, és 4 / 6 mW (2 / 3 mW) teljesítményszinten jelenik meg.
Ebben az esetben a teljes nyereség 4 / 6 = 2 / 3, tehát a kimeneti teljesítmény valójában kisebb lesz, mint a bemeneti teljesítmény.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 dBm

5 ábra - Kaszkádos erősítő erősítés és csillapító.

12 mW + 34 mW + 8 mW + 20 dB

Kiegészítő információk a logaritmusról
A termékek logaritmusai
A fentiekben implicit módon alkalmazott logaritmusok tulajdonsága az alábbiakat állítja, és ez az alapja annak, hogy a logaritmus értékeit összeadjuk és kivonjuk, a lineáris ekvivalenseik megszorozása helyett.

A 'h * j / k * m / n' olyan komponensek kaszkádját jelentheti, amelyek három eszközzel (h, j és m) rendelkeznek, mindegyik erősítéssel> 1 és két eszközzel (k és n), mindegyik erősítéssel <1 6. ábra). A teljes rendszererősítés kiszámítható úgy, hogy megszorozzuk az összes lineáris erősítési értéket, vagy összeadjuk az összes decibel erősítési értéket.

6 ábra - Kaszkádos alkatrészek

Exponensek logaritmusai
Az alábbiak fontosak annak megértéséhez, hogy a teljesítménynövekedés az erő szempontjából 10 * log (Pout / Pin) dB, miközben a teljesítménynövekedés a feszültség szempontjából 20 * log (Vout / Vin) dB.


ami azért van, mert a cf egyenlő c-vel, szorozva önmagában „f” idővel. Például, ha f = 4:


Teljesítmény nyereség teljesítmény alapján vs teljesítmény nyereség a feszültség alapján
A teljesítménynövekedés Pout / Pin, a feszültségnövekedés Vout / Vin. A teljesítmény-nyereséget a decibelben megadott teljesítményarány alapján 10 * log (Pout / Pin) -ként definiálják. A teljesítménynövekedés feszültség szempontjából [(Vout2 / R) / (Vin2 / R)], mivel Ohm törvénye szerint P = V2 / R. A nevezőkben szereplő „R” megszakítja a Vout2 / Vin2 elhagyását, amely megegyezik a (Vout / Vin) 2 értékkel, ahogyan azt az exponens szabálya határozza meg, amely szerint ac / bc = (a / b) c. Ennélfogva:

Fontos megjegyzés: A feszültség szempontjából feszültségnövekedés 10 * log (Vout / Vin) dB, ugyanolyan, mint a teljesítménynövekedésnél. Csak akkor, ha a teljesítménynövekedést feszültségben fejezik ki, akkor érvényes az 20 * log (Vout / Vin) dB egyenlet. Ez egy általános zavaró pont.


A matematikában egyetlen művelet sem önkényes, és ez igaz arra, hogy a jel teljesítményveszteségét (erősítést <1) negatív értékként ábrázolják, és ezért egy kaszkádszámítás során levonják. Egyszerű bemutató, de említésre méltó.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

Ha rádióállomást szeretne építeni, fokozza az FM rádió adóját, vagy bármilyen másra van szüksége FM berendezés, Nyugodtan vegye fel velünk a kapcsolatot: [e-mail védett].

Hagyjon üzenetet 

Üzenetlista