Teljesítmény és amplitúdó: watt, feszültség és hivatkozott decibel

Bevezetés
A rádiófrekvenciás alkalmazásokban (de sok más alkalmazásban is) nagyon gyakori a nagyon nagy és nagyon kis jelek kezelése. Például egy adó-vevő továbbíthatja az 100 W teljesítményét, és csak 10 fW-t (vagy 0.000'000'000'000'01 W) fogadhat. Ezeknek a rendkívül eltérő teljesítményszinteknek ugyanaz az áramköre lehet. Természetesen ezeket az értékeket kifejezhetjük Watt-ban kifejezve a műszaki jelöléssel (mint fentebb) vagy a tudományos jelöléssel, például 1 · 102 W és 1 · 10 – 14 W, ám ezeket meglehetősen nehéz megmondani, és ha az exponens hibásan írta meg , az ebből eredő hiba óriási lesz.

Egy másik módszer a logaritmus átvétele és az összes teljesítmény dBm-ben konvertálása. Az 100 W + 50 dBm és az 10 fW –110 dBm lesz: ezeket az ábrákat sokkal könnyebben lehet kezelni szívből és írni. Ezután, ha a különféle áramköri blokkok csillapítását és nyereségét szintén dB-ben fejezik ki, a végső teljesítmény megtalálásához egyszerűen mindent össze lehet adni a szorzás helyett, és a számítások tovább egyszerűsödnek.

Nem mindenki élvezi a dB, dBm és hasonló (álszereplő) egységeket: nincs szigorú igény ezek használatára, de olyan széles körben használják őket a mérnöki munkában, hogy nagyon nehéz elkerülni őket.

Néhány elmélet
A decibeleket (dB) a teljesítményarányok logaritmikus kifejezésére használják, így a nagyon nagy és nagyon kis teljesítmény összehasonlítható kényelmes számokkal. A decibel dimenzió nélküli álszerep, mert a két teljesítmény aránya határozza meg. Mivel azonban a decibelek annyira praktikusak, hogy a valódi hatalom kifejezésre kerüljenek, nem csak egy méret nélküli arány, a hivatkozott decibelt gyakran használják.

Ha a hatalomról beszélünk, akkor az alábbi egyenlet határozza meg a P teljesítmény d szintet (dB) a W teljesítményben, a p0 teljesítményhez viszonyítva:

Az 10 tényező azért van, mert a decibelek "a Bells tizede". De soha nem hallottam a Bells-ben végzett mérésekről, csak decibeleket használnak.

A leggyakoribb egység a dBm ("dBm" kiejtése), más néven dBmW vagy decibel-milliwatt: ez csak a teljesítményszint dB-ben, összehasonlítva a p0 = 1 mW referenciateljesítménnyel. Időnként dBW-t is használnak, és kifejezik a p0 = 1 W-hoz viszonyítva a teljesítményarányt, de ezek nem nagyon gyakoriak.

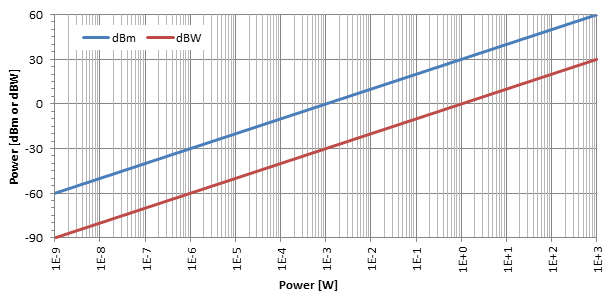
A fenti ábra szerint a decibel-átalakítás logaritmikus hatása nyilvánvaló. Amint láthatjuk ezen a log-lin grafikonon, a dBm és a dBW csak két egyenes, amelyeket az 30 dB választ el egymástól: a dBm átalakításához dBW-ként egyszerűen kivonjuk az 30-t.

Egyes területeken, mint például az analóg TV-vétel, a feszültség mérése a teljesítmény helyett. Ez nem jelent problémát, mindaddig, amíg az impedancia ismert és rögzített (a TV-vevők általában 75 Ω-t használnak).

Az abszolút feszültségek kihasználhatják a decibel-logaritmikus skála előnyeit is, ha decibel-mikrovolt (dBμV) és decibel-volt (dBV). A leggyakoribb a dBμV, amely kifejezi az u0 = 1 μV feszültség arányát. Néha dBV-t is használnak, és kifejezik a feszültség arányát az u0 = 1 V viszonylatában.

Vigyázzon, hogy a feszültségek dB képletükben "20" helyett "10" helyett használják. Ennek oka az, hogy a decibelt mindig teljesítmény-adagként határozzák meg; ha csak feszültségeink vannak, akkor először meg kell osztanunk őket, hogy megtaláljuk az energiát. Ez a kettő teljesítménye, ha kihagyják a logaritmusból, megsokszorozza a meglévő 10 tényezőt az 2-tal.

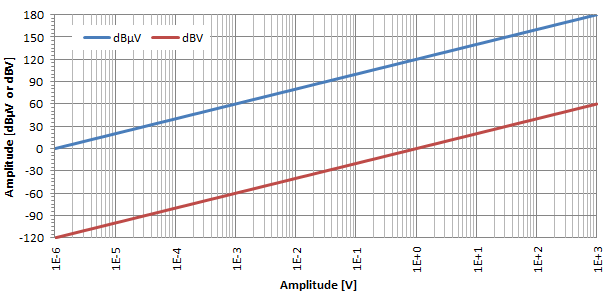
Amint az a fenti ábrán látható és hasonlóan, mint korábban, a decibel-átalakítás logaritmikus hatása a feszültségekre is nyilvánvaló. Amint láthatjuk ezen a log-lin grafikonon, a dBμV és a dBV csak két egyenes, amelyeket az 120 dB választ el egymástól: a dBμV átalakításához dBV-ként egyszerűen kivonjuk az 120-t.

Most, ha át akarjuk váltani az áramellátásról feszültségre és fordítva, akkor tudnunk kell az impedanciát. Csak a következő egyenletet használjuk:

Ez az átalakítás csak akkor érvényes, ha a Zc impedancia valós, és a terhelés hozzá van igazítva az átviteli vonalhoz.

Ha a teljesítményszintet dBm-ben és az amplitúdószintet dBμV-ban ábrázoljuk a teljesítmény függvényében W-ban egy adott impedanciára (itt Zc = 50 Ω), akkor a következőt kapjuk:

Mint korábban, két párhuzamos 107 dB vonal van egymástól. Tehát a dBm-ből dBμV-vé történő konvertáláshoz egyszerűen adjon hozzá 107 dB-t Zc = 50 Ω-hoz, adjon hozzá 109 dB-t Zc = 75 Ω-hoz, adjon hozzá 115 dB-t Zc = 300 Ω-hoz, vagy adjon hozzá 118 dB-t Zc = 600 Ω-hoz.

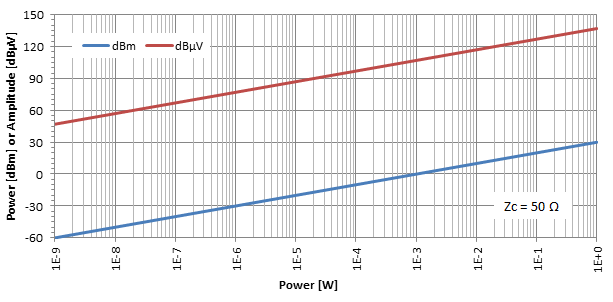
Gyakorlati megfontolások
Első pillantásra gondolhatjuk, hogy a logaritmus miatt feltétlenül szükség van egy zsebszámológépre a dBm kezeléséhez. Valójában egy durva számítás könnyen elvégezhető a fejedben. Csak három tényt kell megjegyeznie:
 Az 1 mW teljesítménye 0 dBm.
 Minden alkalommal, amikor a teljesítmény megduplázódik, add hozzá az 3 dB-t.
 Minden alkalommal, amikor a teljesítmény 10 tényezővel növekszik, add hozzá az 10 dB értéket.

Nézzük meg néhány példát: Tegyük fel, hogy 26 dBm teljesítményszinttel rendelkezik. Írhatunk 26 dBm = 0 dBm + 10 dB + 10 dB + 3 dB + 3 dB, és az előző három szimbólumszabályokkal könnyen megtalálhatjuk az energiát 1 mW · 10 · 10 · 2 · 2 = 400 = XNUMX = XNUMX = XNUMX .

Egy másik példa: tegyük fel, hogy van -33dBm: felírhatjuk a -33 dBm = 0 dBm - 10 dB - 10 dB - 10dB - 3 dB, és azt látjuk, 1 mW / 10 / 10 / 10 / 2 = 0.5 mW.

Ez másképp működik is, például az 50 mW csak 1 mW · 10 · 10 / 2. DBm-ben 0 dBm + 10 dB + 10 dB –3 dB = 17 dBm.

Ehhez némi gyakorlat szükséges, de ezt nagyon könnyű megtenni. Nem olyan pontos, mint a zsebszámológép, mert csak ± 2 dB-nél lehet pontos, de erőfeszítésként nagyon jó képet ad a jel erősségéről.

Hasonló módszer működik a dBμV esetében is, de a szabályok eltérnek:
 Az 1 μV amplitúdója 0 dBμV.
 Minden alkalommal, amikor az amplitúdó megduplázódik, add hozzá az 6 dB-t.
 Minden alkalommal, amikor az amplitúdó 10 tényezővel növekszik, adjunk hozzá 20 dB-t.

Meglepődhet a korábban bemutatott decibelszámításokban, ahol a dB hozzáadódik a dBm-hez, ami elég furcsa. Ennek oka az, hogy a decibelek ál-egységek, és nem a szokásos módon viselkednek. A két teljesítmény aránya dB-ben van kifejezve, de mérete nélkül: például az 3 dB csak "kétszer annyit" jelent. A dBm-ben kifejezett teljesítmény valóban egy hatalom: például az 10 dBm azt jelenti, hogy "10-szor erősebb, mint az 1 mW", ami 10 mW.

Most, amikor decibelt (dB, dBm, ...) adunk hozzá, logaritmikus jellegük miatt valójában megszorozzák az eredeti számadatokat. Tehát, ha hozzáad egy 3 dB nyereséget az 10 dBm teljesítményhez, akkor megkapja az 13 dBm értéket. De amit tényleg tettél, az 2 tényezőt megszorozzuk az 10 mW teljesítménnyel, így 20 mW-t kapunk, amely 13 dBm!

Eddig olyan jó, hogy a hozzáadást sokkal könnyebb megtenni a fejedben, mint a szaporodást, és ez a decibelt olyan praktikussá teszi. De van egy probléma: mivel a decibelek összeadása megfelel az eredeti tényezők szorzásának, hogyan lehet összeadni (kombinálni) két jel teljesítményét? Nos, nem tudod. Nem adhat hozzá dBm-et a dBm-hez. Ha például van egy olyan áramköre vagy készüléke, amely egyesíti az 10 dBm (10 mW) jel teljesítményét egy másik 13 dBm (20 mW) jel teljesítményével, akkor az eredmény 10 mW + 20 mW = 30 mW, amely 14.8 dBm. Ezt nem lehet közvetlenül dBm-ben megtenni, mindkét energiát Watts-ban konvertálni kell, össze kell őket adni és visszaadni dBm-ben. Ez a decibel korlátozása és a közös bukás; szerencsére ez a művelet nem túl gyakori.

Ha rádióállomást szeretne építeni, fokozza az FM rádió adóját, vagy bármilyen másra van szüksége FM berendezés, Nyugodtan vegye fel velünk a kapcsolatot: [e-mail védett].

Hagyjon üzenetet 

Üzenetlista